Paso a paso desarrollo de un videojuegos con C++ y SFML Parte II
Un videojuego sencillo en C/C++ y SFML
Parte II
El tamaño de cada rectángulo debe ser aproximadamente de 65.3 píxeles de ancho para que quepan en 800 píxeles separados uno del otro a una distancia de a/4 es decir unos 16,32 píxeles.
Ya tenemos el tamaño de cada ladrillo (a) hecho a la medida gracias a la matemáticas y no por prueba y error, que probablemente nos tomaría mas tiempo para llegar al tamaño idóneo del ladrillo y la separación para que todo cuadre.
Un ladrillo tiene forma rectangular, por ello podemos establecer que su altura sea la mitad de su ancho, es decir a/2 = 32,65.
Cada uno de los rectángulos van a tener una coordenada variable que llamamos x, y una coordenada fija llamada y, y que será siempre igual a cero (y=0). El primer rectángulo se dibujará en la coordenada (0,0) y el segundo lo dibujaremos separado del primero a una b parte de su ancho mas el ancho del primer rectángulo, es decir, en la coordenada (a + a/b , 0) (2), si b = 4 entonces la coordenada es (a + a/4, 0) que simplificando nos da (5a/4 , 0). El tercer rectángulo se ubicara a la medida de dos rectángulos mas la medida de dos separaciones es decir a 5a/4 + 5a+4 o simplemente 2*(5a/4) = 10a/4; la coordenada del tercer rectángulo sería igual a (2*5a/4) , 0) y así sucesivamente como vemos en el siguiente gráfico:
sf::RectangleShape ladrillo(sf::Vector2f(65, 32))
ladrillo.setPosition(0,0);
ventana.draw(ladrillo);
Los tres paso anteriores debemos repetirlos tantos ladrillos tengamos que dibujar. Como vemos no sería la manera más eficiente si tenemos que dibujar 100 o mas rectángulos.Pero lo anterior se puede resolver utilizando las sentencias de control de flujo while o for.
while (ventana.isOpen()) {
// sección de código a ejecutar hasta que
// la condición sea cierta , en este caso
// si la ventana està abierta
}
La sentencia for (para) tiene una estructura un poco diferente a la de while y la vamos a utilizar para dibujar los 10 rectángulos en la ventana.
int x = 0;
int y = 0;
for (int i = 0; i < 10; ++i){
x = i * 82;// calculamos la coord x de cada ladrillo
ladrillo.setPosition(x, y);
ventana.draw(ladrillo);
}
Parte II
En la primera parte logramos tener dos objetos en movimiento, e interactuando en pantalla, un circulo y un rectángulo. El circulo que simula una pelota (no esta regida por la fuerza de gravedad) y se mueve entre los limites de la ventana. En la parte inferior, el limite lo establece el rectángulo el cual es manejado por el jugador. Establecimos la condición de que si ambas áreas tanto la del circulo como la del rectángulo se interceptan (colisión) se produce el rebote de lo contrario perdemos una vida o se produce el Game Over.
Logrado lo anterior avanzamos al siguiente nivel. En esta parte vamos a colocar en la parte superior de la ventana un conjunto de rectángulos que vamos a llamar ladrillos orientados horizontalmente. Dichos ladrillos se van destruir al ser tocados por la pelota. En los antiguos juego de la Atari, el conjunto de rectángulo estaba conformado por varias filas y columnas.Primero vamos a colocar una fila de rectángulos y después filas y columnas. En la tercera parte vamos al almacenar cada rectángulo en un arreglo (array) bidimensionales y luego para tener filas y columnas lo haremos con arreglos multidimensionales.
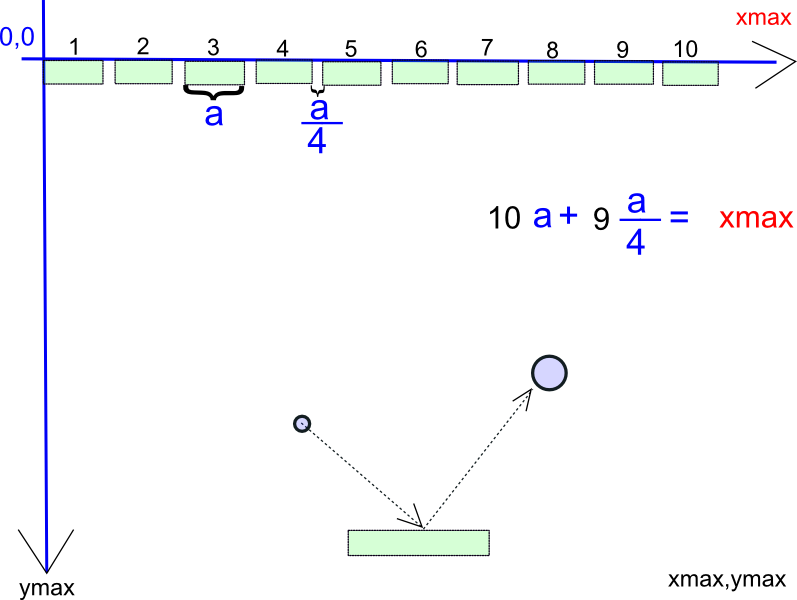
Los juegos de vídeos se ejecutan en diferentes pantallas con diferentes resoluciones. Dichas resoluciones tienen un limite horizontal o ancho (xmax) y otro vertical o alto (ymax) como vemos en la imagen siguiente:
Logrado lo anterior avanzamos al siguiente nivel. En esta parte vamos a colocar en la parte superior de la ventana un conjunto de rectángulos que vamos a llamar ladrillos orientados horizontalmente. Dichos ladrillos se van destruir al ser tocados por la pelota. En los antiguos juego de la Atari, el conjunto de rectángulo estaba conformado por varias filas y columnas.Primero vamos a colocar una fila de rectángulos y después filas y columnas. En la tercera parte vamos al almacenar cada rectángulo en un arreglo (array) bidimensionales y luego para tener filas y columnas lo haremos con arreglos multidimensionales.
Los juegos de vídeos se ejecutan en diferentes pantallas con diferentes resoluciones. Dichas resoluciones tienen un limite horizontal o ancho (xmax) y otro vertical o alto (ymax) como vemos en la imagen siguiente:
Calculando el tamaño de los rectángulos.
Para nuestro juego debemos definir la cantidad de ladrillos que vamos a colocar por fila, y también la distancia a la cual van a estar separados el uno de otro. Teniendo definida la cantidad de ladrillos y la separación entre ellos, lo siguiente es aplicar una sencilla ecuación de una incógnita para calcular el ancho del ladrillo (a). Como vemos en el ejemplo de la figura anterior, si queremos colocar 10 ladrillos separados por la cuarta parte de su largo, la ecuación para calcular cuanto debe medir cada rectángulo o ladrillo es:
10a + 9.a/4 = xmax
Donde a es nuestra incógnita que representa el largo del triangulo y xmax ancho máximo de la resolución de la pantalla. Como vemos el número de separaciones entre los ladrillos es la cantidad de ladrillos menos uno, por ello podemos establecer una ecuación mas general donde n es la cantidad de ladrillos y n - 1 la cantidad de separaciones, a/b es la distancia de la separación y xmax el ancho de la pantalla.
n.a + (n - 1). a/b = xmax
Si nuestro vídeo juego va a correr en una resolución de 800x600, y queremos colocar 10 rectángulos separados por una cuarta parte de su ancho podemos calcular el tamaño de cada rectángulo despejando a:
a = xmax * b / b.n + n - 1 (1)
Donde :
xmax = 800, n = 10, b = 4;
a = 800*4 / 4*10 + 10 - 1
a = 3200 / 49
a = 65,3
a = xmax * b / b.n + n - 1 (1)
Donde :
xmax = 800, n = 10, b = 4;
a = 800*4 / 4*10 + 10 - 1
a = 3200 / 49
a = 65,3
El tamaño de cada rectángulo debe ser aproximadamente de 65.3 píxeles de ancho para que quepan en 800 píxeles separados uno del otro a una distancia de a/4 es decir unos 16,32 píxeles.
Muchas personas se pregunta hace falta utilizar matemáticas para programar vídeo juegos. La repuesta es sí. A pesar que ya hay muchas cosas escritas que se pueden reutilizar, debemos tener en cuenta que hay una gran cantidad de trabajo que debemos hacer, y la matemáticas nos será muy útil para conseguir nuestros objetivos. Los vídeos juegos tratan de emular el mundo real, o un mundo imaginario (ambos basados en nuestra percepción del mundo real). Para poder emular los fenómeno naturales o comportamiento de algún objeto en una computadora, debemos realizar abstracciones del mundo real. Dichas abstracciones llevan siglos desarrollándose en la matemáticas y están a la disposición en ecuaciones, formulas teoremas, etc. listas,para ser usadas en nuestro código fuente. Espero que lo anterior no sea un motivo para desanimarse sino al contrario, un estimulo para aprender hacer las cosas mejor usando las matemáticas.
Un ladrillo tiene forma rectangular, por ello podemos establecer que su altura sea la mitad de su ancho, es decir a/2 = 32,65.
Como dibujar una secuencia de rectángulos en la pantalla.
Teniendo las medidas del ladrillo o rectángulo (65,3 x 32,65), la próxima tarea es saber como dibujar todos los ladrillosCada uno de los rectángulos van a tener una coordenada variable que llamamos x, y una coordenada fija llamada y, y que será siempre igual a cero (y=0). El primer rectángulo se dibujará en la coordenada (0,0) y el segundo lo dibujaremos separado del primero a una b parte de su ancho mas el ancho del primer rectángulo, es decir, en la coordenada (a + a/b , 0) (2), si b = 4 entonces la coordenada es (a + a/4, 0) que simplificando nos da (5a/4 , 0). El tercer rectángulo se ubicara a la medida de dos rectángulos mas la medida de dos separaciones es decir a 5a/4 + 5a+4 o simplemente 2*(5a/4) = 10a/4; la coordenada del tercer rectángulo sería igual a (2*5a/4) , 0) y así sucesivamente como vemos en el siguiente gráfico:
Como ya conocemos el valor de a, es decir el ancho del rectángulo que es igual a a=65,3 y la separación de uno del otro a/4= 16,32 en total a + a/4 = 81,62 redondeando queda en 82. Luego lo sustituimos en la ecuación para conseguir la coordenada x de cada rectángulo:
x0 = 0*82 , y0 = 0 coordenadas = ( 0, 0)
x1 = 1*82 , y1 = 0 coordenadas = ( 82, 0)
x2 = 2*82 , y2 = 0 coordenadas = (164, 0)
x3 = 3*82 , y3 = 0 coordenadas = (246, 0)
.
.
.
x9 = 9*82 y9 = 0 coordenadas = (738 , 0)
xn = n * a + a/b ---> ( n * (a + a/b) , yn ) (2)
Los ladrillos se pueden dibujar uno por uno con la siguientes instrucciones:
x0 = 0*82 , y0 = 0 coordenadas = ( 0, 0)
x1 = 1*82 , y1 = 0 coordenadas = ( 82, 0)
x2 = 2*82 , y2 = 0 coordenadas = (164, 0)
x3 = 3*82 , y3 = 0 coordenadas = (246, 0)
.
.
.
x9 = 9*82 y9 = 0 coordenadas = (738 , 0)
xn = n * a + a/b ---> ( n * (a + a/b) , yn ) (2)
Los ladrillos se pueden dibujar uno por uno con la siguientes instrucciones:
Primero, creamos un objeto rectangular con las medidas 65 de ancho por 32 de alto, segundo le damos una posición dentro de la ventana creada, y por último dibujamos en la pantalla creada el rectángulo llamado ladrillo.
ladrillo.setPosition(0,0);
ventana.draw(ladrillo);
Los tres paso anteriores debemos repetirlos tantos ladrillos tengamos que dibujar. Como vemos no sería la manera más eficiente si tenemos que dibujar 100 o mas rectángulos.Pero lo anterior se puede resolver utilizando las sentencias de control de flujo while o for.
Sentencias de control de flujo:
La sentencia while (mientras que) ya la utilizamos anteriormente para ejecutar repetidamente una sección de código hasta que una condición dada es verdadera. Dicha condición prueba constantemente si la ventana está abierta. Si la ventana esta abierta (verdadero) el bloque de instrucciones que encierra el bloque while se ejecuta.while (ventana.isOpen()) {
// sección de código a ejecutar hasta que
// la condición sea cierta , en este caso
// si la ventana està abierta
}
La sentencia for (para) tiene una estructura un poco diferente a la de while y la vamos a utilizar para dibujar los 10 rectángulos en la ventana.
int x = 0;
int y = 0;
for (int i = 0; i < 10; ++i){
x = i * 82;// calculamos la coord x de cada ladrillo
ladrillo.setPosition(x, y);
ventana.draw(ladrillo);
}
Como vemos el de una sentencia for tiene un encabezado compuesto de tres partes: una sentencia de inicialización (int i = 0) , una condición ( i < 10), y una expresión (++i). EL encabezado controlan como se ejecuta el cuerpo que se encuentra dentro del las llaves {}. La instrucciones dentro del cuerpo se ejecutan 10 veces y el valor de i empieza en 0 se incrementa en cada ciclo con la sentencia ++i, alcanzando un valor máximo de 9 permitido por la condición i < 10.
Para llevar todo lo anterior a la practica vamos a escribir un pequeño programa usando la generalidad de la ecuación para que dibuje n cantidad de ladrillos separados a la razon de a/b, con la resolución que coloquemos en las variables xmax y ymax:
#include <SFML/Graphics.hpp>
int main()
{
int xmax = 800, ymax = 600;
int n = 20; // Numeros de ladrillos
double b = 4; // Razon de separacion entre ladrillos
double a = (xmax*b) / (b*n + n - 1);// aplicando (1) calcula el ancho de cada ladrillo
double x = 0, y = 0; // coordenadas inciales de los ladrillos
sf::RenderWindow ventana(sf::VideoMode(xmax, ymax), "Ventana @intellvirtual ");
sf::RectangleShape ladrillo(sf::Vector2f(a, a/2));//objeto ladrillo ancho = a, alto = a/2
while (ventana.isOpen())
{
sf::Event event;
while (ventana.pollEvent(event))
{
if (event.type == sf::Event::Closed)
ventana.close();
}
ventana.clear();
for (int i = 0; i < n; ++i){
x = i * (a + a/b);// aplicamos (2) calculamos la coord x de cada ladrillo
ladrillo.setPosition(x, y);
ventana.draw(ladrillo);
}
ventana.display();
}
return 0;
}
En la próxima parte construiremos filas y columnas de ladrillos con arrays multidimensionales. Si este curso te ha sido de ayuda y estas interesado en continuar, escríbenos y deja tu comentarios...
int main()
{
int xmax = 800, ymax = 600;
int n = 20; // Numeros de ladrillos
double b = 4; // Razon de separacion entre ladrillos
double a = (xmax*b) / (b*n + n - 1);// aplicando (1) calcula el ancho de cada ladrillo
double x = 0, y = 0; // coordenadas inciales de los ladrillos
sf::RenderWindow ventana(sf::VideoMode(xmax, ymax), "Ventana @intellvirtual ");
sf::RectangleShape ladrillo(sf::Vector2f(a, a/2));//objeto ladrillo ancho = a, alto = a/2
while (ventana.isOpen())
{
sf::Event event;
while (ventana.pollEvent(event))
{
if (event.type == sf::Event::Closed)
ventana.close();
}
ventana.clear();
for (int i = 0; i < n; ++i){
x = i * (a + a/b);// aplicamos (2) calculamos la coord x de cada ladrillo
ladrillo.setPosition(x, y);
ventana.draw(ladrillo);
}
ventana.display();
}
return 0;
}
Y para n = 30:
En la próxima parte construiremos filas y columnas de ladrillos con arrays multidimensionales. Si este curso te ha sido de ayuda y estas interesado en continuar, escríbenos y deja tu comentarios...






Comentarios
Publicar un comentario